Parking Lot Questions for Test 2

• How do you do 30-60-90 and 45-45-90 triangles?

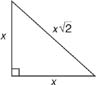  Your legs for a 45-45-90 are always going to be the same. x=x
                              The hypotenuse is always going to be the leg times square root of two.


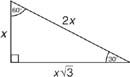   Your hypotenuse is always twice the length of your shorter leg. (Shorter leg is half the length of hypotenuse).

                                   The longer leg is always the shorter leg times square root of three.

• What is the definition of trigonometric ratio?

The definition of trigonometric ratio is a ratio of the lengths of sides of a right triangle. (SOH-CAH-TOA)

• What is a Pythagorean Triple?

A Pythagorean Triple is just three WHOLE NUMBERS that satisfy the Pythagorean Theorem.

• What is the geometric mean?

The geometric mean between two numbers satisfies the proportion a/x=x/b, where x is your geometric mean between the numbers a and b.

The altitude of a right triangle is the geometric mean between the lengths of the two segments it breaks the hypotenuse into.

The side of a right triangle is the geometric mean between the length of the segment of the hypotenuse adjacent to the side and the length of the whole hypotenuse.

• When do you use geometric mean and special right triangles?

Whenever you have a right triangle, and the angles are labeled 45-45-90, or 30-60-90, (Or if you know it is a special right triangle. For example, on number 9 on the study guide, it told you that you had a square with a diagonal. You should know that the diagonal of a square cuts the square into two 45-45-90 triangles), always use your rules for special right triangles (listed above)

Whenever you do not have enough information to use the Pythagorean Theorem (you do not know two sides of the right triangle) or you are not dealing with a special right triangle, you can use the rules for the geometric mean (listed above).

• What is a good way to help remember the different ways of solving for geometric mean?

 The picture below shows how the altitude of a right triangle splits that triangle into two similar triangles. This is why these proportions work. Hope this helps!